基础视觉SLAM教程

一.例子

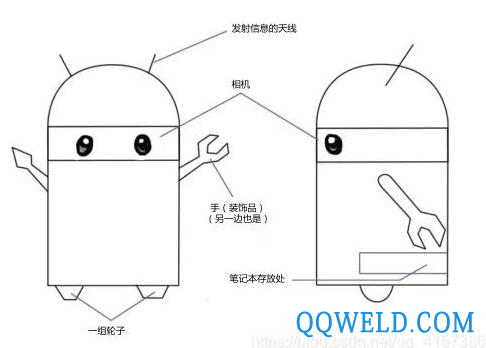
如上图的小萝卜机器人，要使其具有自主运动能力至少需要两个条件：

1. 我在什么地方？——定位。

2. 周围环境是什么样？——建图。

因此它既需要知道自身的状态-位置，也要了解所在的环境-地图。解决这些问题的方法非常多，如携带于机器人本体上的传感器，例如机器人的轮式编码器、相机、激光等等，另一类是安装于环境中的，例如导轨、二维码标志等等。

 二.相机

在视觉SLAM中主要是用相机去解决定位与建图问题。按照相机的工作方式，把相机分为单目（Monocular）、双目（Stereo）和深度相机（RGB-D）三个大类，如下图所示。直观看来，单目相机只有一个摄像头，双目有两个，而 RGB-D 原理较复杂，除了能够采集到彩色图片之外，还能读出每个像素离相机的距离。它通常携带多个摄像头，工作原理和普通相机不尽相同。此外，SLAM 中还有全景相机 、Event 相机  等特殊或新兴的种类。

单目相机 ：

只使用一个摄像头进行 SLAM 的做法称为单目 SLAM（Monocular SLAM）。这种传感器结构特别的简单、成本特别的低，所以单目 SLAM 非常受研究者关注，它的数据格式就是常见的照片。

照片本质上是拍照时的场景（Scene），在相机的成像平面上留下的一个投影。它以二维的形式反映了三维的世界。显然，这个过程丢掉了场景的一个维度：也就是所谓的深度（或距离）。在单目相机中，我们无法通过单个图片来计算场景中物体离我们的距离（远近）——之后我们会看到，这个距离将是 SLAM 中非常关键的信息。由于我们人类见过大量的图像，养成了一种天生的直觉，对大部分场景都有一个直观的距离感（空间感），它帮助我们判断图像中物体的远近关系。比如说，我们能够辨认出图像中的物体，并且知道它们大致的大小；比如近处的物体会挡住远处的物体，而太阳、月亮等天体一般在很远的地方；再如物体受光照后会留下影子等等。这些信息可以都帮助我们判断物体的远近，但也存在一些情况，这个距离感会失效，这时我们无法判断物体的远近以及它们的真实大小。由于单目相机只是三维空间的二维投影，所以，如果我们真想恢复三维结构，必须移动相机的视角。

在单目 SLAM 中也是同样的原理。我们必须移动相机之后，才能估计它的运动（Motion），同时估计场景中物体的远近和大小，称之为结构（Structure）。如果相机往右移动，那么图像里的东西就会往左边移动——这就给我们推测运动带来了信息。另一方面，我们还知道近处的物体移动快，远处的物体则运动缓慢。于是，当相机移动时，这些物体在图像上的运动，形成了视差。通过视差，我们就能定量地判断哪些物体离得远，哪些物体离的近。

单目 SLAM 估计的轨迹和地图，将与真实的轨迹、地图，相差一个因子，也就是所谓的尺度（Scale）。由于单目 SLAM 无法仅凭图像确定这个真实尺度，所以又称为尺度不确定性。

单目相机数据

双目相机 (Stereo) 和深度相机 ：

双目相机和深度相机的目的，在于通过某种手段测量物体离我们的距离，克服单目无法知道距离的缺点。如果知道了距离，场景的三维结构就可以通过单个图像恢复出来，也就消除了尺度不确定性。尽管都是为测量距离，但双目相机

与深度相机测量深度的原理是不一样的。双目相机由两个单目相机组成，但这两个相机之间的距离（称为基线（baseline））是已知的。我们通过这个基线来估计每个像素的空间位置——这和人眼非常相似。我们人类可以通过左右眼图像的差异，判断物体的远近，在计算机上也是同样的道理。如果对双目相机进行拓展，也可以搭建多目相机，不过本质上并没有什么不同。

双目相机数据

深度相机数据

总结：

单目相机：以二维的形式反应了三维的世界，丢掉了深度，也就是物体到我们的距离。

双目相机：克服了单目相机的深度问题，通过已知两眼间的距离后大量计算。

深度相机（RGB-D）:克服了深度问题。原理是通过激光传感器，通过主动向物体发射光并接收返回的光，测出物体离相机的距离，节省了大量计算，存在的问题是范围窄，视野小，易受日光干扰。

 三.经典视觉SLAM框架

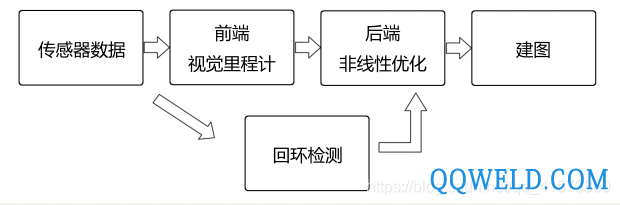
整个视觉 SLAM 流程分为以下几步：

1. 传感器信息读取。在视觉 SLAM 中主要为相机图像信息的读取和预处理。如果在机器人中，还可能有码盘、惯性传感器等信息的读取和同步。

2. 视觉里程计 (Visual Odometry, VO)。视觉里程计任务是估算相邻图像间相机的运动，以及局部地图的样子。VO 又称为前端（Front End）。

3. 后端优化（Optimization）。后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对它们进行优化，得到全局一致的轨迹和地图。由于接在 VO 之后，又称为后端（Back End）。

4. 回环检测（Loop Closing）。回环检测判断机器人是否曾经到达过先前的位置。如果检测到回环，它会把信息提供给后端进行处理。

5. 建图（Mapping）。它根据估计的轨迹，建立与任务要求对应的地图。

四.SLAM问题的数学表述

假设小萝卜正携带着某种传感器在未知环境里运动，怎么用数学语言描述这件事呢？

首先，由于相机通常是在某些时刻采集数据的，所以我们也只关心这些时刻的位置和地图。这就把一段连续时间的运动变成了离散时刻 t = 1, . . . , K当中发生的事情。在这些时刻，用 X 表示小萝卜自身的位置。于是各时刻的位置就记为 X1, . . . ,Xk，它们构成了小萝卜的轨迹。地图方面，我们设地图是由许多个路标（Landmark）组成的，而每个时刻，传感器会测量到一部分路标点，得到它们的观测数据。不妨设路标点一共有 N个，用 Y1, . . . ,YN表示它们。在这样设定中，“小萝卜携带着传感器在环境中运动”，由如下两件事情描述：

1. 什么是运动？我们要考虑从 k -1 时刻到 k 时刻，小萝卜的位置 x 是如何变化的。

2. 什么是观测？假设小萝卜在 k时刻，于Xk处探测到了某一个路标Yj，我们要考虑这件事情是如何用数学语言来描述的。

通常，机器人会携带一个测量自身运动的传感器，比如说码盘或惯性传感器。这个传感器可以测量有关运动的读数，但不一定直接是位置之差，还可能是加速度、角速度等信息。然而，无论是什么传感器，我们都能使用一个通用的、抽象的数学模型：

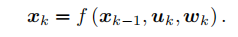
这里uk是运动传感器的读数（有时也叫输入），wk为噪声。注意到，我们用一个一般函数 f 来描述这个过程，而不具体指明 f的作用方式。这使得整个函数可以指代任意的运动传感器，成为一个通用的方程，而不必限定于某个特殊的传感器上。我们把它称为运动方程。与运动方程相对应，还有一个观测方程。观测方程描述的是，当小萝卜在 xk位置上看到某个路标点yj，产生了一个观测数据 zk,j。同样，我们用一个抽象的函数h 来描述这个关系：

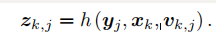
这两个方程描述了最基本的 SLAM 问题：当我们知道运动测量的读数u，以及传感器的读数 z 时，如何求解定位问题（估计 x）和建图问题（估计 y）？这时，我们把 SLAM问题建模成了一个状态估计问题：如何通过带有噪声的测量数据，估计内部的、隐藏着的状态变量。

状态估计问题的求解，与两个方程的具体形式，以及噪声服从哪种分布有关。按照运动和观测方程是否为线性，噪声是否服从高斯分布进行分类，分为线性非线性和高 斯非高斯系统。其中线性高斯系统（Linear Gaussian, LG 系统）是最简单的，它的无偏的最优估计可以由卡尔曼滤波器（Kalman Filter, KF）给出。而在复杂的非线性非高斯系统（Non-Linear Non-Gaussian，NLNG 系统）中，我们会使用以扩展卡尔曼滤波器（ExtendedKalman Filter, EKF）和非线性优化两大类方法去求解它。